Introduction
Biofilms are highly organized, microbial communities that can develop on biotic or abiotic surfaces (Costerton et al., 1987; Costerton et al., 1999). Microbial biofilms can be found almost everywhere, and also in industrial and clinical environments (Tsai, 2005). Biofilms are a severe problem for human health (for only pathogenic microorganisms) and industry because they are highly resistant to antimicrobial agents, sanitizers, and biocides, and are particularly difficult to eliminate after the maturation phase (Costerton et al., 1987; Cvitkovitch et al., 2003; Mah et al., 2003).
Microorganisms found on moist surfaces in food processing environments can easily attach to many surfaces to form microcolonies and produce biofilms (Wirtanen et al., 1996). The development of biofilms in food processing environments leads to continuous contamination of products. Food biofilms may contain both pathogenic microorganisms that can cause infectious diseases and spoilage microorganisms that decline the food quality (Boulange-Peterman, 1996). Microorganisms in biofilms can be protected from sanitation agents used in clean-in-place (CIP) procedures because the possibility of survival for the cells in biofilms is higher than the planktonic counterparts. Inadequate routine sanitation procedures against food biofilms lead to shorter shelf-life of foods and the spread of foodborne diseases (Bower et al., 1996). Also, biofilm-associated extracellular polymeric substances termed as the matrix that holds the cells in biofilms together cannot be removed by sanitation procedures, and enable the development of biofilms for newly arrived microorganisms (Stewart et al., 1997). The formation of biofilm may also hinder the heat transfer and cause corrosion on metal surfaces where the products are processed (Chmielewski and Frank, 2003).
Thermophilic bacilli such as Anoxybacillus flavithermus and Geobacillus spp. are contaminants for the dairy industry (Burgess et al., 2009). Although Geobacillus stearothermophilus is one of the most common Geobacillus species in dairy product manufacture, Geobacillus thermodenitrificans, and G.thermoglucosidans may also pose risks for this industry. G. thermodenitrificans can be a contaminant for heat-treated food products and can produce biofilm in simulated dairy conditions (Karaca et al., 2019; Manachini et al., 2000). G. themoglucosidans can be isolated from the end product in the units where dairy products are processed, and it is known as a problematic biofilm former (Cho et al., 2018; Zhao et al., 2012).
These thermophilic bacilli are non-pathogenic; however, their presence in dairy products may be indicative of poor hygiene, and high numbers are unacceptable to food quality and market sales. The development of thermophilic bacilli in products leads to a significant decrease in the quality of the product due to acid and enzyme production (Marchand et al., 2012). Also, the spores of obligate thermophiles are more resistant to heat than the spores of mesophilic bacteria in milk flora (Sadiq et al., 2016). Spores of heat resistant thermophiles cannot be inactivated by almost any process (Cho et al., 2018). The durable biofilms of thermophilic bacilli also cause the constantly multiplying bacteria, spores, and heat resistant enzymes to be released into the dairy units (Sadiq et al., 2017). Product processing conditions in the dairy industry are capable of selectively promoting the development of thermophilic bacilli. These bacilli can quickly multiply in sections where temperatures reach 40°C–68°C in dairy production facilities (Flint et al., 2001). Besides, they are challenging to eliminate because they are spore formers. They also tend to grow very rapidly (generation time of approximately 15–20 min) and are capable of quickly forming biofilms (Ronimus et al., 2003; Scott et al., 2007).
It is known that routine sanitation strategies for eliminating, preventing, or delaying thermophilic bacilli biofilm formation in dairy environments may not be sufficient. In addition, it is known that the application of sodium hydroxide, preferred in routine sanitation processes in the product processing units in the dairy industry, is not sufficient for the removal of Anoxybacillus and Geobacillus contaminants (Wedel et al., 2019). In order to develop better control mechanisms, the link between the production of thermophilic biofilms and the conditions of the dairy environment where the products are processed needs to be better understood (Bremer et al., 2006; Marchand et al., 2012; Parkar et al., 2003; Parkar et al., 2004). Predictive microbiology allows defining the behavior of microorganisms under defined conditions, but only if the responses of microorganisms to environmental factors can be repeated. The prediction of the growth of microorganisms affected by different environmental factors can be beneficial for evaluating the food safety and shelf life of food products (McMeekin et al., 1993). In order to benefit from predictive microbiology applications in the food industry, there is a need for appropriate mathematical models that consistently define microbial behavior. There are several preferred sigmoid equations and various models for the development kinetics of microorganisms. Each of these models differs in terms of "ease of use" and the number of parameters in the equation. Comparisons of mathematical and statistical suitability criteria of different growth models are essential for the construction of more useful models (Baty and Delignette-Muller, 2004; Buchanan et al., 1997; López et al., 2004; Zwietering et al., 1990).
Temperature and incubation time are the most important parameters that should be taken into consideration in order to estimate the biofilm development of thermophilic bacilli in the dairy environment. Modeling could be a powerful technique by means of studying the effects of primary conditions such as temperature and time on thermophilic bacilli biofilms and reconsidering process conditions in terms of minimizing thermophilic biofilm risks. Thus, the objective of this study was to describe the biofilm formation of Geobacillus and Anoxybacillus in whole milk on stainless steel surfaces at different temperature levels for various incubation times by using mathematical models.
Materials and Methods
G. thermodenitrificans DSM 465T, G. thermoglucosidans B84a and A. flavithermus DSM 2641T strains were provided from Ankara University, Microbiology Research Laboratory of Biology Department, Turkey. These bacteria are influential biofilm formers in dairy products (Karaca et al., 2019). All reference strains were stored at –86°C in MI broth [composed of 0.5% peptone (Sigma-Aldrich, St. Louis, MO, USA), 0.3% yeast extract (Merck), 0.3% K2HPO4 (Sigma-Aldrich), 0.1% KH2PO4 (Sigma-Aldrich)] cultures supplemented with 20% glycerol (Suzuki et al., 1976).
Culture enrichment procedures were performed before the experiments, as described by Kilic et al. (2017). This inoculation process was crucial in terms of stimulating biofilm formation of the thermophilic bacilli. Briefly, a colony of each thermophilic bacilli culture on tryptic soy agar (TSA; Merck) were transferred into tryptic soy broth (TSB; Merck) and incubated at 55°C for 18 h (6×g). These cultures were then inoculated into fresh TSB and grown at 55°C for an additional 6 h.
The biofilms were sampled and screened at three temperatures (55°C, 60°C, and 65°C) for different incubation times (up to 144 h) to determine the biofilm production responses on 316 L type stainless steel surfaces. The biofilms were sampled with 10% reconstituted dry whole milk (Sigma-Aldrich) which had been autoclaved at 121°C for 5 min before (Somerton et al., 2015).
The study was performed based on a 6-well microtiter plate layout. As an abiotic surface, specially cut stainless steel (316 L) surfaces were preferred (R: 7 mm, total surface area; 3.08 cm2). These surfaces were treated with some cleaning and sterilization procedures such as detergent, acetone treatments, rinsing, and autoclaving in order to remove possible organic residues. The surfaces were initially treated with isopropanol overnight and agitated with a chlorinated detergent (Presept effervescent disinfectant tablets, Johnson & Johnson, Paranaque City, Philippines) for 30 min. The coupons were then rinsed with deionized water and autoclaved before use. Inoculation preparation of the thermophilic bacilli was carried out, as previously stated (Kilic et al., 2017). Sterile surfaces were planted into each well of the microtitre plate in duplicate. The wells were then filled with 5 mL of sterile standard whole milk, and active cultures were inoculated into these contents (4% v/v; approximately 107 CFU/mL). The plates were sealed to hinder evaporation and incubated at given incubation temperatures under static conditions. At the end of each incubation period, the wells were emptied under aseptic conditions, and the surfaces removed. The surfaces rinsed with sterile physiological saline (0.9% NaCl) to remove planktonic counterparts. The surfaces were placed in a sterile plastic tube containing 5 mL of physiological saline and 3 g of glass beads (R: 3 mm) to detach the biofilm cells. The tubes were then vortexed for 2 min at maximum intensity. For total bacterial counts, ten-fold dilutions in physiological saline were prepared, and each dilution was dropped in 10 μL onto TSA (Merck) agar plates. The plates were incubated at 55°C for 24 h before colony counting. The results were calculated as colony-forming units per unit area (CFU/cm2) and then converted to the logarithmic base (Log10CFU/cm2). The colony-forming unit detection limit of the preferred method for counting biofilm cells is approximately 1.5 Log10CFU/cm2. All the experiments were done at least in duplicate (Burgess et al., 2014; Karaca et al., 2019). The sampled thermophilic biofilms on stainless steel surfaces were also confirmed by Confocal Scanning Laser Microscopy (Carl Zeiss Microscopy, Thornwood, NY, USA). It was possible to analyze biofilm samples of thermophilic bacilli in standard whole milk. It was also clearly observed that the current biofilm dispersing method used was efficient in harvesting the biofilm cells of thermophilic bacilli, and the efficacy of the method was confirmed by the crystal violet method (results not shown).
The biofilm formation data of G. thermodenitrificans and G. thermoglucosidans was described by using the hyperbolic equation Eq. (1):
where N(t) is the number of bacteria in CFU/cm2 on stainless steel surface at a time t, Nmax is the maximum cell number attained during the stationary period, and th is the time to reach log10Nmax/2. It was assumed that when t = 0 log10N(t) = 0 indicating that number of cells attached initially on the surface was low in numbers.
Since the lag time was observed, different models were used for A. flavithermus. The first model was hyperbolic equation with lag Eq. (2):
where tlag is the lag time in h.
The second model was the Gompertz equation Eq. (3) proposed by Zwietering et al. (1990):
where A is the maximum cell number in Log10CFU/cm2 attained during the stationary period, μm is the maximum biofilm formation rate in Log10CFU/cm2·h, and λ is the lag time in h. Although this model is widely used to describe the microbial growth curves, it could also be possible to use the modified Gompertz equation Eq. (3) to describe the biofilm formation of bacteria (Karaca et al., 2013; Speranza et al., 2011).
The third model was the Baranyi Eq. (4) which model consists of two rate equations (Baranyi and Roberts, 1994):
where , m is the curvature or shape parameter which is, in general, assumed to be 1 for simplicity, and Nmax is the maximum cell density. The term q(t)/[1+q(t)] is associated with the lag time (λ) through the introduced parameter h0 = μmax·λ which appears in the solution of the rate equation (Peleg and Corradini, 2011). Therefore, it could be possible to obtain both a maximum biofilm formation rate (μmax) and lag time (λ) by solving these two differential equations.
The last model used was the three-phase linear model Eq. (5) proposed Buchanan et al. (1997):
where tmax is the time to reach maximum population density (log10Nmax), and μ is the biofilm formation rate.
Results
The biofilm formation data of G. thermodenitrificans and G. thermoglucosidans indicated that rapid biofilm formation occurred in the first few hours. As time passed, the biofilm formation rate decreased and became zero. A suitable model for this initially fast biofilm-producing followed by a stationary period can be the hyperbolic equation Eq. (1).
Fig. 1 and Fig. 2 show both the biofilm formation data and model fits of G. thermodenitrificans and G. thermoglucosidans, respectively. A rapid initial biofilm formation rate was observed for G. thermodenitrificans, i.e., more than 3 Log10CFU/cm2 was obtained on stainless steel within 4 h (Fig. 1). The biofilm rate was slower for G. thermoglucosidans compared to G.thermodenitrificans: more than 3 Log10CFU/cm2 was obtained on stainless steel within 8 h (Fig. 2).
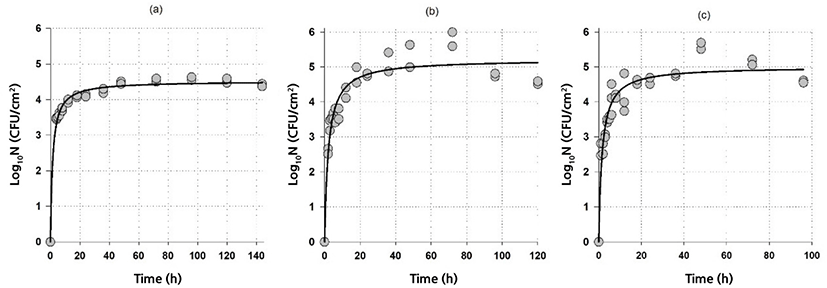
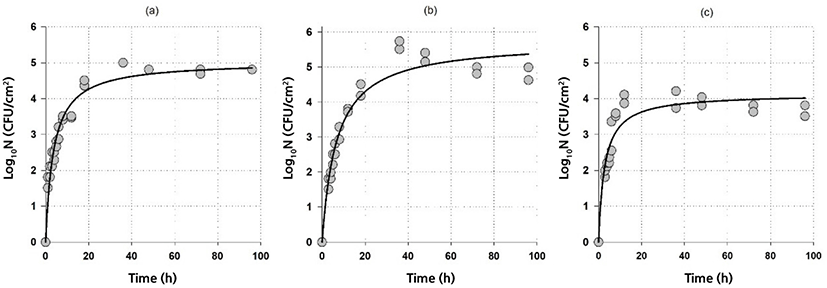
The goodness-of-fit of the model and model parameters are given in Table 1. It could be said that the model with a relatively high adjusted coefficient of determination (R2adj≥0.87) and relatively low RMSE (≤0.39) values could be used to describe the biofilm formation data of Geobacillus spp. The highest log10Nmax observed at 60°C for both G. thermodenitrificans and G. thermoglucosidans were 5.2 and 5.8 Log10CFU/cm2, respectively indicating Geobacillus spp. had higher biofilm production at 60°C than those of 55°C and 65°C. On the other hand, higher counts were observed at 65°C compared to 55°C for G. thermodenitrificans. In contrast, just the opposite was obtained for G. thermoglucosidans (see Figs. 1 and 2, and log10Nmax values in Table 1). It could also be possible to calculate the biofilm formation rate by assuming a linear relationship for the rapid initial stage and by using the parameters given in Table 1. Since th is the time to reach log10Nmax/2, biofilm formation rates can be calculated as log10Nmax/(2×th). The calculated formation rates are listed in Table 2. Note that biofilm-producing rates for G. thermodenitrificans were much higher than the biofilm-producing rates of G. thermoglucosidans, and highest biofilm-producing rates were observed at 65°C for both bacteria. The formation of the high amount of biofilm did not necessarily indicate a higher biofilm formation rate since the highest biofilm amount was observed at 60°C for both bacteria (Table 1). However, the biofilm formation rate was the lowest at this temperature (Table 2).
| T (°C) | μ (Log10CFU/cm2·h) | |
|---|---|---|
| G. thermodenitrificans | G. thermoglucosidans | |
| 55 | 1.54 | 0.69 |
| 60 | 1.22 | 0.43 |
| 65 | 1.59 | 0.74 |
The same hyperbolic trend was also observed biofilm formation of A. flavithermus except that there was a lag time for the formation. The very same model Eq. (1) with lag time integrated Eq. (2) was also used to describe the biofilm formation of A. flavithermus since hyperbolic growth with lag was observed.
Table 3 shows the R2adj and RMSE values of the models used for describing the biofilm formation of A. flavithermus. Although all models produced reasonable fits, the hyperbolic equation with lag was superior based on R2adj and RMSE values. Note that the modified Gompertz Eq. (3), the Baranyi Eq. (4), and three-phase linear Eq. (5) models produced almost the same fits (results not shown). Moreover, Baranyi model had the convergence failure at 55°C, which was not surprising since the biofilm formation data of A. flavithermus is not the same as the expected microbial growth: after the lag period, a rapid biofilm formation was observed.
Fig. 3 shows the fit of the hyperbolic equation with lag Eq. (2) and the modified Gompertz equation Eq. (3) to the biofilm formation data of A. flavithermus in whole milk on stainless steel. Since Gompertz Eq. (3), Baranyi Eq. (4) and three-phase linear Eq. (5) models were overlapped, only the fit of Gompertz Eq. (3) are shown in Fig. 3.
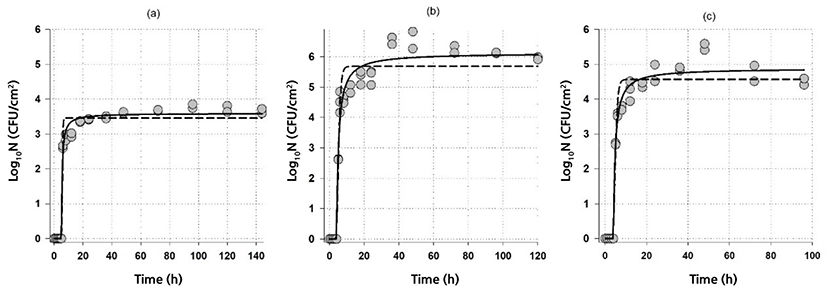
Comparison of the parameters of both models revealed (Table 4) that although similar parameter values were obtained, the hyperbolic equation with lag Eq. (2) had the highest maximum biofilm cell number, Gompertz equation Eq. (3) had the highest biofilm formation rate. In contrast, the three-phase linear had the lowest rate. All the models had almost identical lag time values (Table 4). Moreover, calculated formation rates from Eq. (2) (3.59, 2.7 and 2.8 Log10CFU/cm2·h at 55°C, 60°C, and 65°C, respectively) were also similar to that of obtained from Gompertz equation (Table 4). Biofilm formation rates of A. flavithermus were much higher than the biofilm formation rates of G. thermodenitrificans and G. thermoglucosidans, indicating that after the lag period A. flavithermus could proliferate on stainless steel.
The highest biofilm cell number was obtained at 60°C followed by 65 and 55°C (see Fig. 3. and also see parameters in Table 4). Similarly, the same bacteria in whole milk had higher biofilm formation on stainless steel (about 4 Log10CFU/cm2) at 65°C than that of 55°C (about 2 Log10CFU/cm2) (Karaca et al., 2019). It should be noted that th was defined as the time to reach log10Nmax/2 in h; however, since there was lag time for A. flavithermus tlag + th was required to reach the half of the maximum cell number. Hence, 5.5, 5.1, and 4.9 h were needed to reach 1.8, 3.1, and 2.4 Log10CFU/cm2 at 55°C, 60°C, and 65°C, respectively.
Discussion
Although the attachment of different bacteria to stainless steel surfaces at different temperatures has been shown, the biofilm formation of thermophilic bacilli under various conditions is still limited. The genus Geobacillus and Anoxybacillus can adhere to various surfaces such as polyvinyl chloride, polypropylene, polystyrene, polycarbonate, glass, and stainless steel, and form biofilm on these surfaces. Among them, stainless steel is widely used material by the dairy industry (Karaca et al., 2019). Furthermore, residuals of milk during processing may remain on different parts of the stainless steel equipment and hence forms a thin layer. This layer, which is rich in nutrients, makes the stainless steel surfaces more susceptible to bacterial adhesion and biofilm formation (Silva et al., 2018). Therefore, the biofilm formation of these bacteria in whole milk on stainless steel was investigated in this study. A recent study indicated that both Anoxybacillus and Geobacillus in whole milk produced a high amount of biofilm (>4 Log10CFU/cm2) on stainless steel at 65°C while at 55°C higher formation was observed (>4 Log10CFU/cm2) on glass surfaces (Karaca et al., 2019). In this study, a new temperature level (60°C) was added, and the highest amount of biofilm was observed at this temperature (Figs. 1 and 2, and Table 1).
On the other hand, since microbial growth models such as Gompertz, Baranyi, and three-phase linear models could also be used to describe such data (data with the lag), these models were also tried. Although the Gompertz equation Eq. (3) is widely used to describe the microbial growth curves, it could also be possible to use to describe the biofilm formation of bacteria (Karaca et al., 2013; Speranza et al., 2011).
There is a contradiction in the literature as to which model is the most suitable for describing the microbial growth data, and the choice of a model in predictive food microbiology is often subjective. However, there are many studies regarding the consistency and applicability of the mentioned models for the microbial growth prediction. Gompertz, Baranyi, Richards, logistic, and three-phase linear models are the most widely used models (Coroller et al., 2012; Jewell, 2012; Huang, 2013; López et al., 2004) and these models could be used for biofilm development modeling as well. Tsai (2005) described the accumulation of microorganisms on surfaces in water distribution systems underflow with a logistic model. The attachment patterns of foodborne pathogens such as Listeria monocytogenes, Shigella boydii, Staphylococcus aureus, and Salmonella Typhimurium was estimated by using the modified Gompertz model under the effect of NaCl treatment by Xu et al. (Karaca et al., 2013; Xu et al., 2010). Response surface modeling is another commonly used method to mimic potential industrial food‐processing conditions for evaluating the physiological requirements of biofilm formation (Goeres et al., 2005; Speranza et al., 2011). In this study, however, the hyperbolic equation with lag was the best model among the alternatives to describe the biofilm formation of A. flavithermus since the highest R2adj, and lowest RMSE values were obtained.
This study showed that mathematical modeling could be a useful tool to describe the biofilm formation of thermophilic bacilli in milk on stainless steel. The hyperbolic equation for Geobacillus and hyperbolic equation with lag for Anoxybacillus could successfully be used to describe the biofilm formation. It should be noted that the findings of this study may not be generalized to the genera Geobacillus and Anoxybacillus since biofilm formation can be intensely strain specific even within a single species. However, the procedure can be extended to different bacteria in different foods on various surfaces. Further studies may also focus on dynamic rather than static conditions. Moreover, modeling and predicting the biofilm formation under dynamic conditions may open new doors and would be beneficial for the food industry.













