Introduction
Lactobacillus species are the most frequently and safely used probiotics. It is even commonly consumed by children and immunocompromised individuals (Borriello et al., 2003). In particular, Lactobacillus plantarum, a member of the hetero-fermentative group of Lactobacilli, is a heterogeneous and versatile species that is encountered in a variety of environmental niches, including silage, sourdough, fish, and many fermented vegetables (Seddik et al., 2017). Traditionally, L. plantarum was not used in yogurt fermentation, but it was used in fermented sausages and some types of cheese. According to a recent report, L. plantarum L67, which has a high survival rate at low pH, was found to have been mixed with lactic acid bacteria as a starter culture and could be used for making yogurt (Song et al., 2016).
The species of L. plantarum exhibits various biological effects, including antitumor, anticoagulant, antiviral, immunomodulatory, anti-inflammatory, antidiabetic, antioxidative, and free radical-scavenging activities (Andersson et al., 2010; Giardina et al., 2014).
In a previous study (Jeong et al., 2015), we determined that L. plantarum JNU 2116, isolated from kimchi, has a high survival rate at low pH. Strain JNU 2116 produces an anticarcinogenic peptide (NH2-XLEXKKAEXITTXX) in the presence of mutagens (4-nitroquinoline 1-oxide, N-methyl-N'-nitro-N-nitrosoguanidine, and 2-amino-3-methylimidazole quinoline).
The growth of lactic acid bacteria is greatly affected by the fermentation conditions, such as temperature, pH, medium components, and oxygen, among which the types of growth medium play an important role in bacterial viability. For growing lactic acid bacteria, MRS and M17 media, as well as skim milk, are used extensively. Tryptone, a medium component produced by the digestion of milk caseins by trypsin (Fraser and Powell, 1950), provides an excellent source of amino acids and small peptides for growing microorganisms and is therefore commonly incorporated into the growth media of lactic acid bacteria and other microorganisms.
In order to use probiotics as a health supplement, the fermentation process is a critical factor in large-scale production for enhancing the cell yield (Maÿyra-Mäkinen and Bigret, 1993). Thus, the evaluation of the medium ingredients should be carried out for fermentation optimization. Oh et al. (1995) suggested that a modified response surface (RS) model with cubic and quartic terms could find a more optimal point and thus could assess factor effects more appropriately.
In this study, using a new RS modeling approach, we evaluated the effects of the four medium components that are soy-peptone, glucose, yeast extract, and magnesium sulfate, and estimated the optimum growth conditions for enhancing viable cells of L. plantarum JNU 2116.
Materials and Methods
A central composite design (Myers et al., 2009) in 6 blocks was used to allocate treatment combinations in this experiment, which consisted of 36 runs and was conducted for 6 days (Table 1). Each of the first 4 blocks, which represented days 1, 2, 3, and 4 of the experiment, contained 4 factorial runs and 2 center runs. Each of the last 2 blocks, which represented days 5 and 6 of the experiment, contained 4 axial runs and 2 center runs.
In this experiment, the response, Log (CFU), was assumed to be under the influence of the 4 medium factors mentioned in the Introduction. To set up a statistical model, we denoted Log (CFU) by Y and determined the coded factor levels as follows:
Table 2 contains the actual factor levels corresponding to the coded factor levels. The observed responses of the treatment combinations are presented in Table 1. Using this design, we could fit a second- or higher-order polynomial regression model to the data.
L. plantarum JNU 2116 was obtained from stock cultures maintained by the Dairy Microbiology Laboratory at Chonnam National University (Gwangju, Korea). L. plantarum JNU 2116 was grown for overnight at 37°C in de Man Rogosa Sharpe broth (1960; MRS) and was subcultured three times prior to use. Stock culture of L. plantarum JNU 2116 was stored at -80°C in 10% (v/v) skim milk containing cryoprotectant. For the enumeration of L. planatrum JNU2116, the appropriate diluted-samples were plated by using MRS agar. The plates were incubated at 37°C for 48 h.
Data were analyzed using SAS software (SAS Korea, SAS® 9.4). SAS/STAT (2013) procedures were used for regression modeling. Optimum conditions were found through SAS data-step programming. The plots were generated by SAS/GRAPH (2013).
Results and Discussion
First, the second-order polynomial regression model containing 4 linear, 4 quadratic, and 6 interaction terms plus 5 dummy variables for 6 blocks was employed by using the RSREG procedure of SAS/STAT. The analysis of variance for evaluation of the second-order model is presented in Table 3.
Table 3 shows that the r2 value of the second-order model was 0.8768 and the lack of fit was significant (p=0.0197). This suggested that this regression model did not accurately represent the data in the experimental region, indicating that cubic terms might have to be included in the model. Thus, a third-order polynomial model containing 4 linear, 4 quadratic, 4 cubic, and 6 interaction terms plus 5 dummy variables for 6 blocks was fitted to the data. Table 4 displays the analysis of variance for this third-order model.
As shown in Table 4, the r2 value of this third-order model was 0.9444, the lack of fit of the model was barely insignificant (p=0.0587) at the 5% level, and interactions were not significant with an F-value less than 1 (p=0.6179). Thus, in anticipation of an improvement of the model, we got rid of the interaction trms in Table 4. Table 5 shows the analysis of variance of this third-order model without interaction terms.
From Table 5, we see that the r2 value of this reduced third-order model was 0.9235, the lack of fit of this model was more insignificant (p=0.0985), and each of the covariate, linear, quadratic, and cubic parts contained at least one significant term. This model had fewer terms than the full second-order model in Table 3, yet it produced a larger r2 value and an insignificant lack of fit. Thus, we used this model as the final one for the medium optimization. The coefficients are given in Table 6, where D1, D2, D3, D4, and D5 were defined as follows: if day=1, then D1=1, D2=0, D3=0, D4=0, D5=0; if day=2, then D1=0, D2=1, D3=0, D4=0, D5=0; if day=3, then D1=0, D2=0, D3=1, D4=0, D5=0; if day=4, then D1=0, D2=0, D3=0, D4=1, D5=0; if day=5, then D1=0, D2=0, D3=0, D4=0, D5=1; and if day=6, then D1=0, D2=0, D3=0, D4=0, D5=0.
Our response surface model is written as
whereIn the equation, Ŷ denotes the predicted value of Y, and for j=1, 2, 3, 4, each f̂ (Xj) denotes an estimate of the original function f(Xj)=βj Xj+βjj Xj2+βjjj Xj3.
For k≧2, a kth-order polynomial effect of the factor Xj is defined as the F-value in testing if all the coefficients of the linear term, the quadratic term, …, and the kth-power term of Xj are zero. To compare the third-order polynomial effects of the factors X1, X2, X3, and X4, we compared the F-values and p-values from testing.
Table 7 contains the results from these tests.
From Table 7, we can see that the F-value for X3 (yeast extract) was the largest (31.67), those for X2 (glucose) and X1 (peptone) were similar in the middle group (7.67 and 5.29, respectively), and that for X4 (magnesium sulfate) was the smallest (2.98). Thus, in relative comparison, the order of the factors according to the magnitude of the third-order polynomial effect is as follows:
Since there were no interaction terms in the final model, we could draw the third-order polynomial effect plots of each factor separately (Fig. 1).
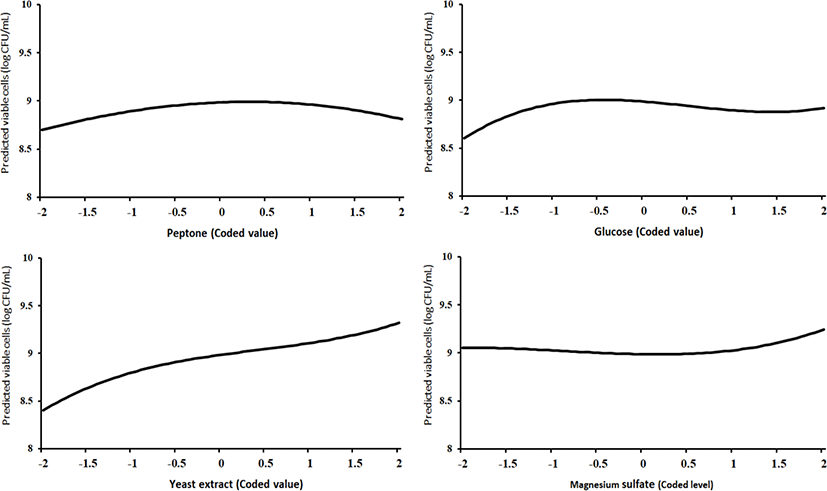
In Fig. 1, the 4 plots depict f̂ (Xj)=bj Xj+bjj Xj2+bjjj Xj3, j=1, 2, 3, 4, respectively, from left to right. The values of bj, bjj, and bjjj, j=1, 2, 3, 4, are given in Table 6. The shapes of these 4 curves were in accordance with the 4 test results in Table 7.
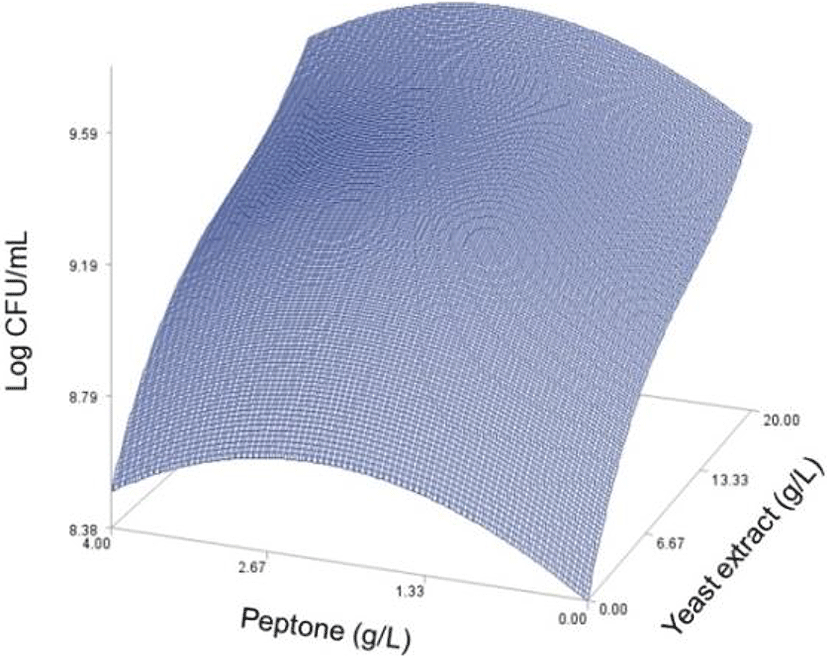
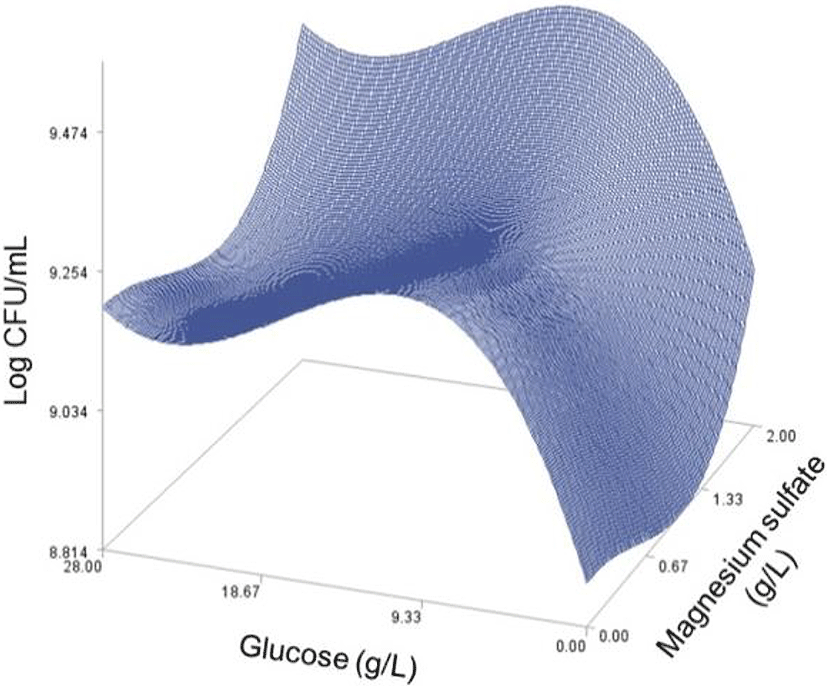
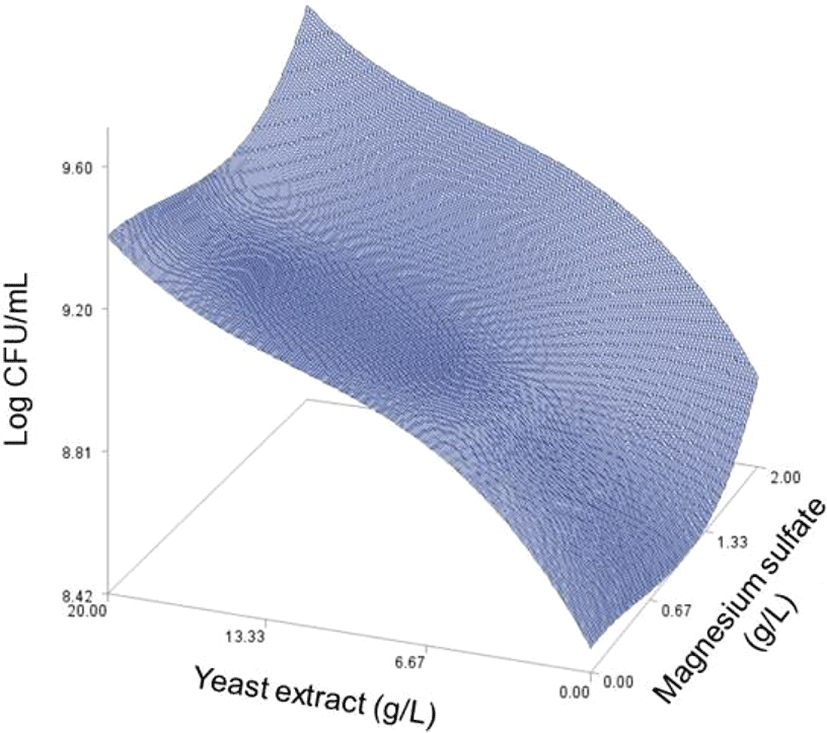
A relative comparison using Fig. 1 also says that the growth of L. plantarum JNU 2116 was affected strongly by yeast extract, moderately by glucose and peptone, and slightly by magnesium sulfate.
Through a search on a grid (Oh et el., 1995), we maximized the predicted response from the model with the coefficients in Table 6, assuming that the values of the block variables were D1=1, D2=0, D3=0, D4=0, and D5=0. The bounds for the factor levels were –2≦Xj≦2, j=1, 2, 3, 4, and the radius of the spherical region of the experimental design displayed in Table 1 was 2. Thus, with the bounds of –2≦Xj≦2, j=1, 2, 3, 4, we made a search within the spherical region with the radius of 2, for which the constraint was X12+X22+X32+X42≦22=4. This search, which was conducted using SAS data-step programming, determined the optimum point, described in Table 8.
| X1 | X2 | X3 | X4 | Distance from the origin | Predicted maximum Log(CFU) | Peptone (g/L) | Glucose (g/L) | Yeast extract (g/L) | Magnesium sulfate (g/L) |
|---|---|---|---|---|---|---|---|---|---|
| 0.13 | –0.24 | 1.94 | –0.4 | 1.9995 | 9.3314 | 2.31 | 12.32 | 19.7 | 0.8 |
A validation experiment was performed to verify the optimization results in Table 8. Table 9 shows the medium composition from the optimization results, which was used for the validation experiment.
To verify the validity of the optimum medium with the composition in Table 9, our validation experiment compared it with MRS broth, a frequently used commercial medium.
The data in Table 9 show that for both media, the number of viable cells was more than 109 (CFU/mL), which is a good result. Our optimum medium turned out to be economically viable in that the price for producing as much as 300 liters of it is as cheap as a little over 100 US dollars, and its cultivation amount is as much as 96.2% that of MRS broth.
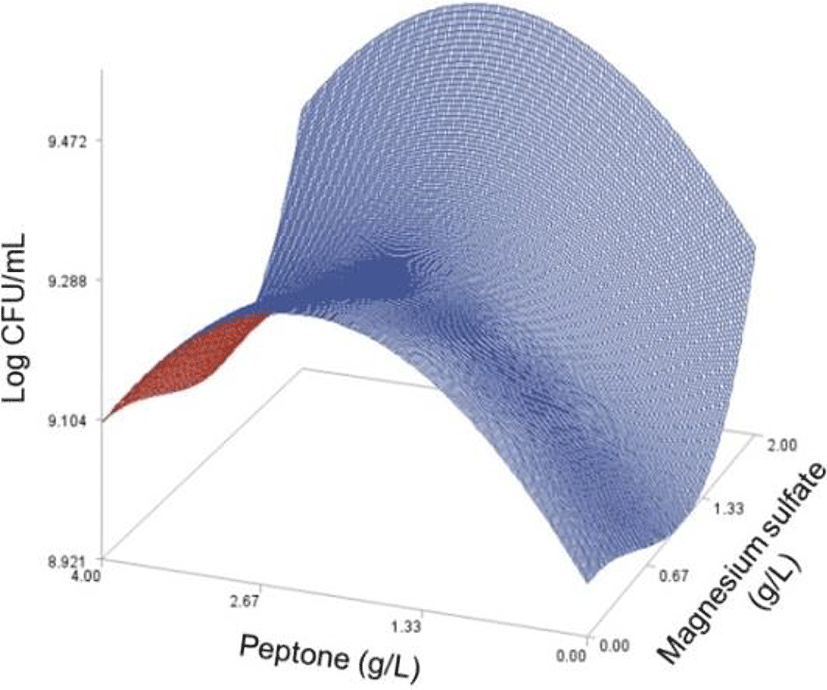
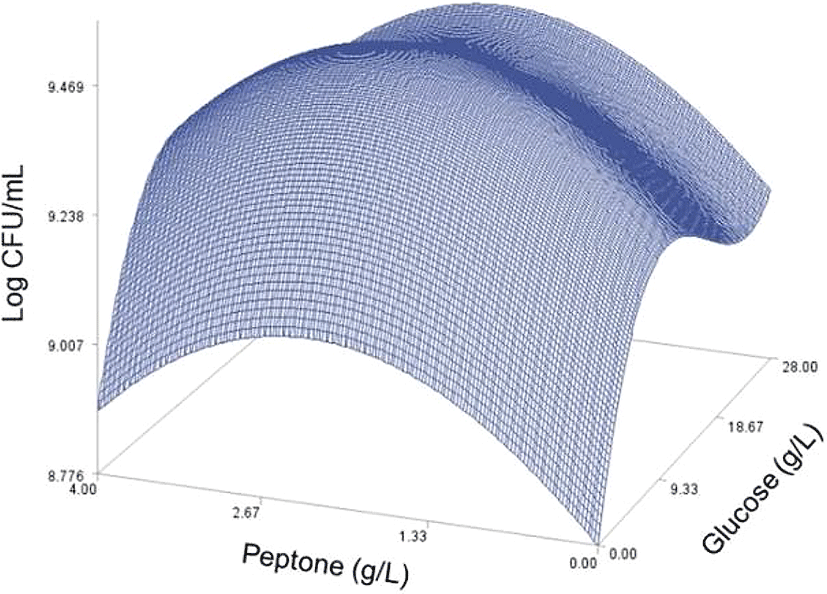
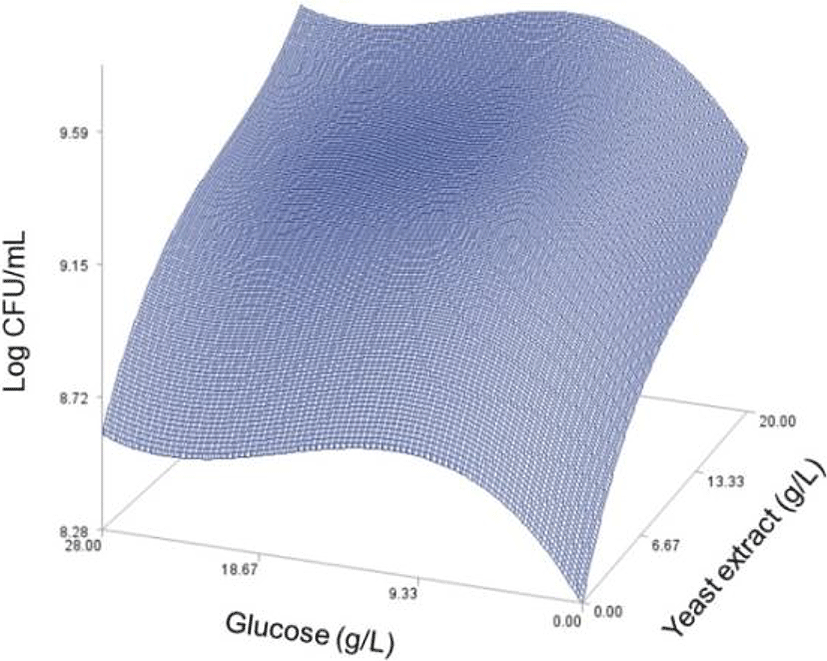
As done in the paper by Oh et el. (1995), for any 2 of the 4 factors, a three-dimensional response surface plot was drawn, with the vertical axis representing the predicted viable cells (Log CFU) and the 2 horizontal axes representing the actual levels of 2 explanatory factors. In these plots, the values of the block variables were set to be D1=1, D2=0, D3=0, D4=0, and D5=0.
In each plot, the factors not represented by the 2 horizontal axes are fixed at their optimum actual levels. From all 6 plots produced (Figs 2 through 7), we can see that the effects of the pairs of the factors were additive since there were no interactions. By the additivity of the 2-factor effects, we mean that the effect of one factor on the response does not depend on the level of the other factors (Oh et al., 1995).
Conclusion
Using a new response surface approach, we developed a statistical model to assess the third-order polynomial effects of the four medium components on the growth of L. plantarum JNU 2116, and established their estimated optimum levels to maximize its growth, which are soy-peptone 0.213%, glucose 1.232%, yeast extract 1.97%, and magnesium sulfate 0.08%, through a validation experiment. Our optimum medium turned out to be economically viable in that its production price is cheaper than that of MRS broth and its cultivation amount is close to that of MRS broth.













